二分探索木 - Rustではじめるデータ構造とアルゴリズム（第2回）

簡単な二分探索木

Rustの特徴のひとつは、所有権(ownership)・移動(move)・借用(borrow)の概念です。これらがコンパイル時に厳格にチェックされることにより、古くから未定義挙動でプログラマを悩ませてきたダングリングポインタなどの問題がなくなり、メモリ安全性がもたらされます。

しかし一方で、自分で多少複雑なデータ構造を定義しようとする場合にはコンパイルを通すだけでもかなりの知識・力量が要求されます。

この（不定期）連載では、 Rustではじめるデータ構造とアルゴリズム と題し、プログラミングコンテストなどでよく見かける基礎的なデータ構造とアルゴリズムを、できるだけシンプルにRustで実装していきます。 &, &mut, Box, Rc, Cell, RefCell などの使い分けや、なぜそれを使う必要があるかの解説を、実例を通して行います。

今回第2回では、 二分探索木 を取り扱います。値の大小に沿った構造を持つ二分木であり、単純なデータ構造でありながら、検索やソートなど実用性が高いです。第1回の二分木に少し制約を付け足した構造になるので、未読の方はぜひ第1回のほうからご覧ください。

連載記事一覧

  1. 二分木
  2. 二分探索木 （この記事）
  3. 平衡二分探索木 （未執筆）
  4. ヒープ （未執筆）
  5. 有向グラフ（ポインタ表現） （未執筆）
  6. 有向グラフ（行列表現） （未執筆）
  7. 無向グラフ（ポインタ表現） （未執筆）
  8. 無向グラフ（行列表現） （未執筆）

目次

二分探索木の説明

二分探索木は二分木の一種です。ただの二分木とは異なり、以下の特性を持っています。

  1. ノードは大小が定義できる値を持つ。
    • 例: 数値, 文字列（辞書順の大小など）
  2. あるノードの左側の子孫ノードは、そのノードの値 以下 の値を持つ。
  3. あるノードの右側の子孫ノードは、そのノードの値 以上 の値を持つ。

どのノードを取っても2, 3 の性質が成立していることが二分探索木の条件です。

簡単な二分探索木

さて、二分探索木の上記の制約は、実は結構緩いです。そのため、同じ値の集合から、異なる複数種類の二分探索木を構成することができます。

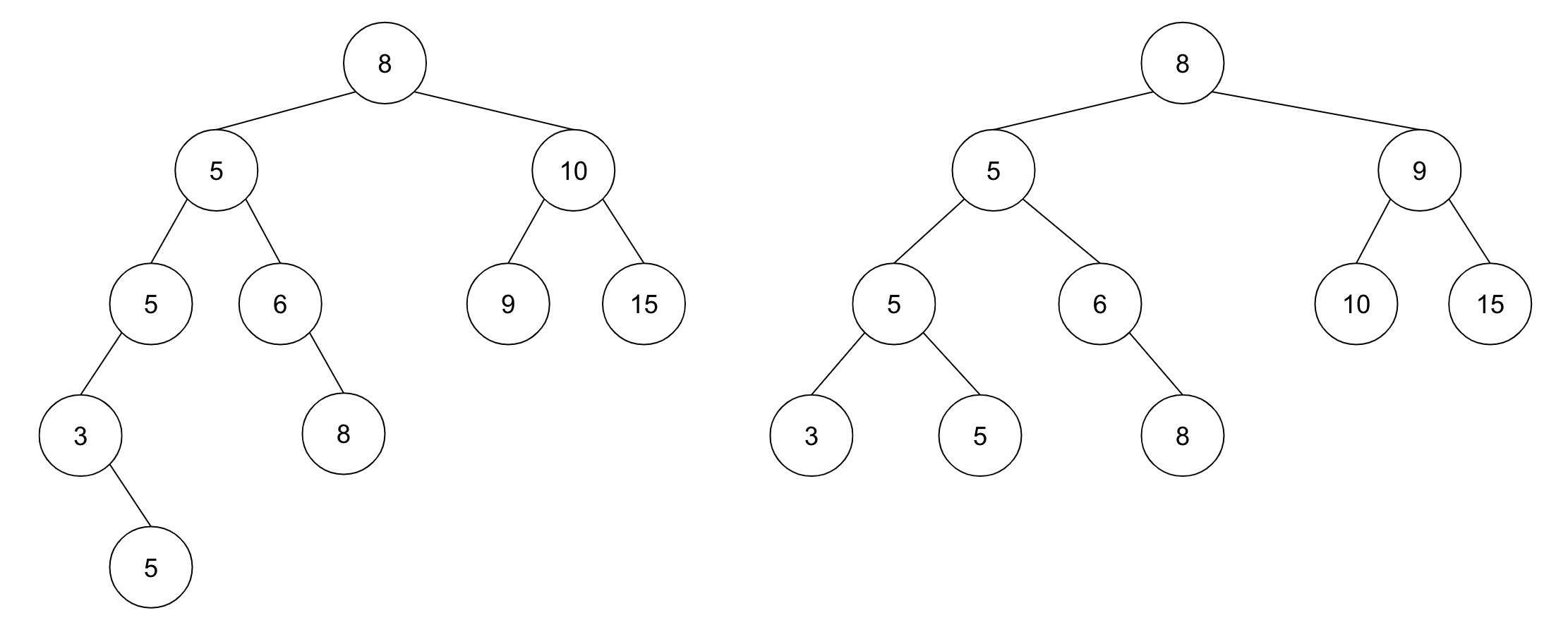
同一の値の集合から異なる二分探索木が構成できる

上の図の2種類の二分探索木は、ともに 3, 5, 5, 5, 6, 8, 8, 9, 10, 15 の値から構成されています。では、どちらが “良い” 二分探索木でしょうか？

それを考えるためには、二分探索木の用途、すなわち関連するアルゴリズムを考える必要があります。

二分探索木のアルゴリズム: 検索

二分探索木の最も基本的な用途は 検索 です。二分 “探索” 木ですものね。
ここでいう検索とは、「パラメータとして指定した値が、二分探索木のどれかのノード値として含まれているかを判定する」操作とします。

二分探索木の要素が n 個、二分探索木の最大の深さが h だとすると、検索操作は O(h) の時間計算量で完了できます。
（ O(xxx) は ビッグオー記法 です）
二分探索木の全要素数ではなく、深さの h しか計算量が掛からないため、比較的高速に検索ができるデータ構造と言えます。

では、どのような手続きで O(h) で検索をするのでしょうか。まずは、冒頭の二分探索木から 6 を探す例を見てみます。

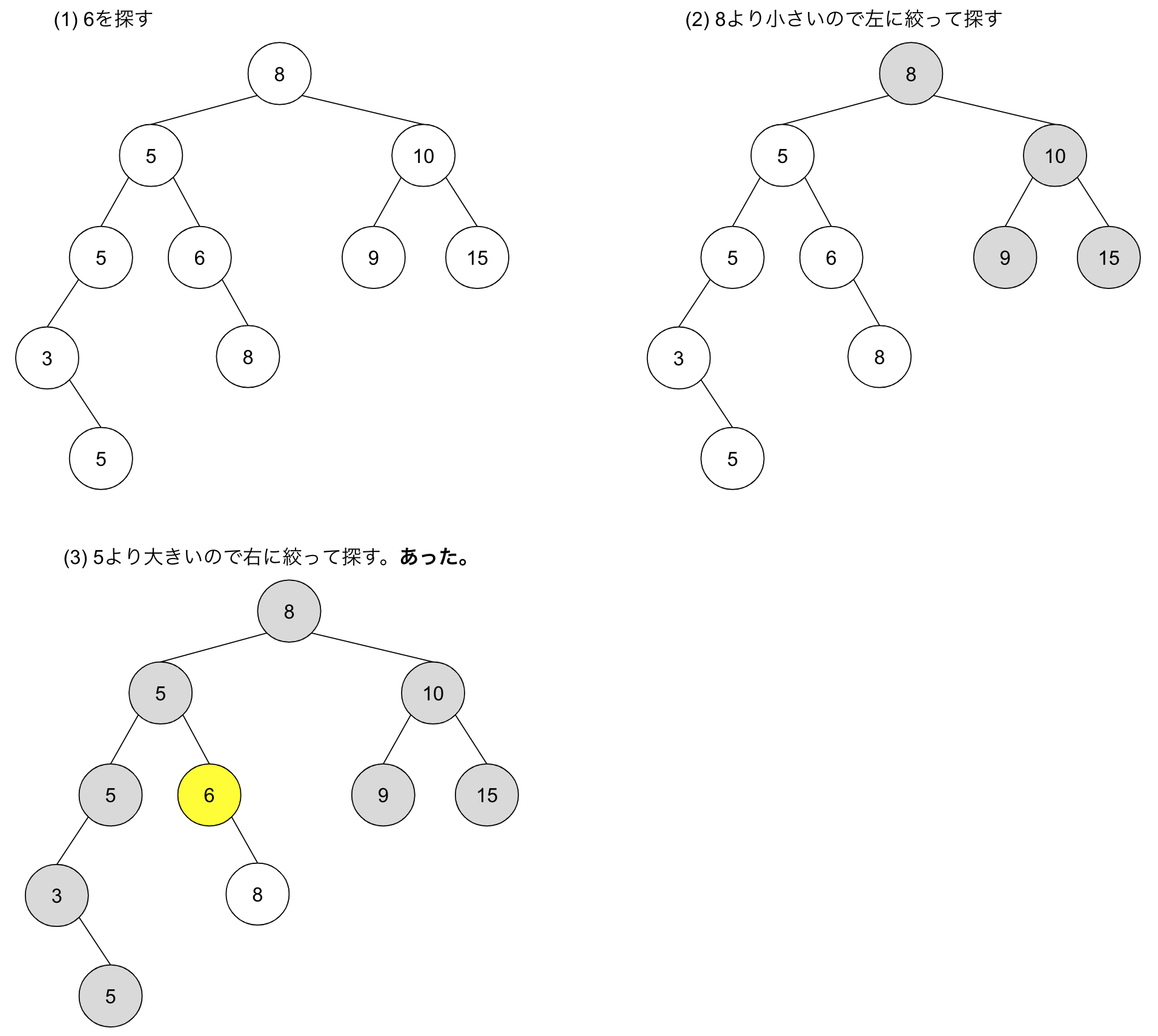
二分探索木から6を検索

二分探索木は左右の子が大小関係に対応しているので、左右のどちらかの可能性を捨てながら深さ優先探索していくことが可能です。検索して見つからない例として、 11 を探す例を見てみます。

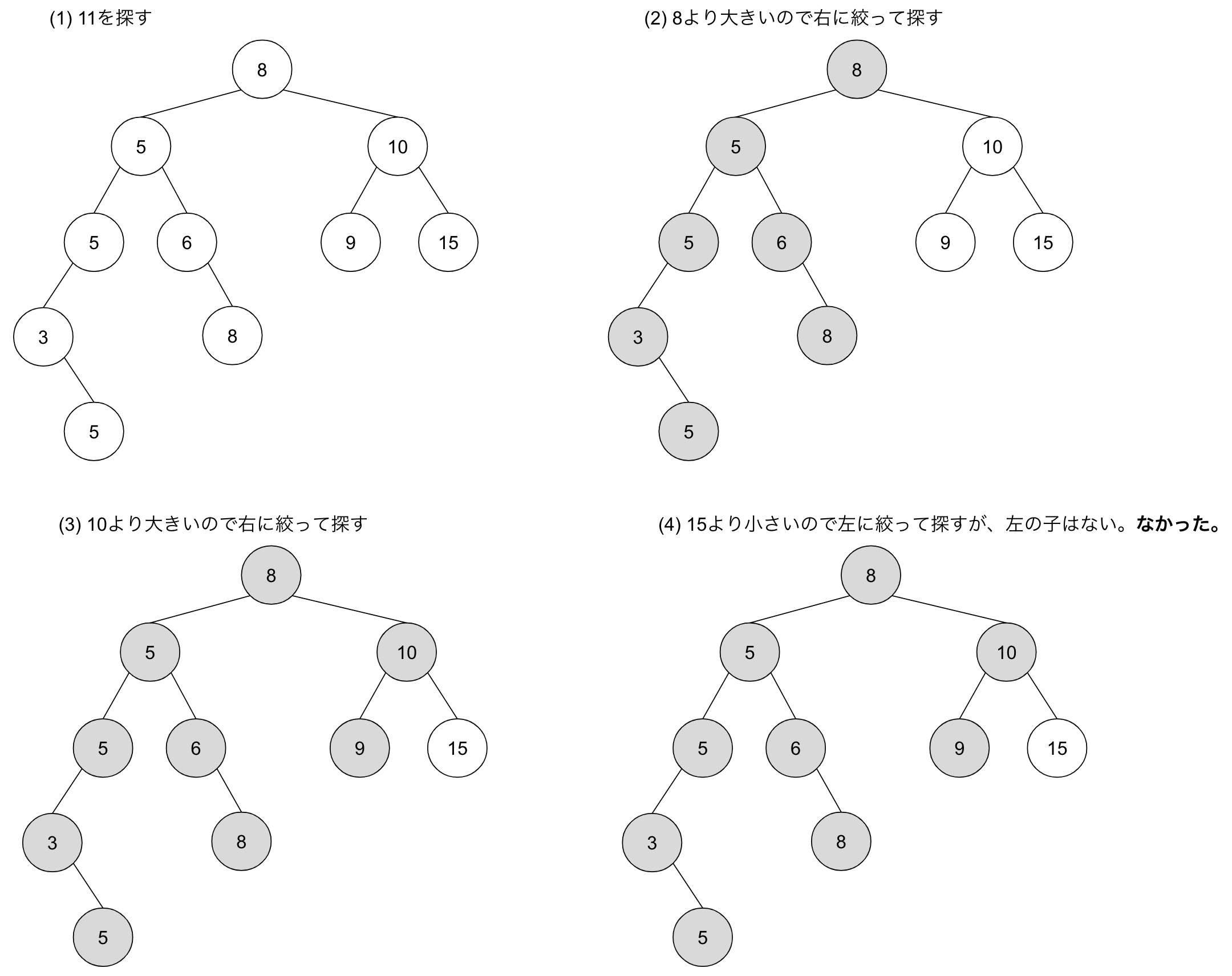
二分探索木から11を検索

探索は必ずリーフまで続ける必要があります。 11 より大きい 15 に当たったからといって探索を停止してはいけません。先程の 6 を探す例も、 6 より小さい 5 を見つけても右への探索を続けたから 6 にたどり着きました。

以上の例からわかるように、各深さごとに1個のノードを見れば十分なので、 O(h) での探索が可能です。では先程の疑問、「 “良い” 二分探索木とはなにか」に戻りましょう。
最大の深さ h が小さければ小さいほど、「一番深いところまで見に行かないと検索に引っかからない」という最悪の場合における計算量が小さくなります。

同一の値の集合から異なる二分探索木が構成できる

従ってこちらの図では、最大の深さが5の左の二分探索木よりも、最大の深さが4の右の二分探索木のほうが、検索効率が良いという点で優れています。

左の二分探索木の最大の深さが大きくなってしまっているのは、バランスが取れていないからです。実は二分探索木は、どんな値の集合を持とうとも、「任意のリーフ同士の深さの差が1以内」になるように構成できます。このようにバランスが取れている（平衡している）二分探索木を 平衡二分探索木 と呼びます。上図の右は、リーフの深さが3か4なので平衡二分探索木ですね。

次回第3回で平衡二分探索木を取り上げますが、今回は平衡ではない二分探索木について説明を続けていきます。

二分探索木のアルゴリズム: 範囲検索

二分探索木では、値の存在の有無を調べる 一致検索 は O(h) ( h は最大の深さ) の時間計算量であることを見ました。しかし一致検索だけならハッシュテーブルなどは O(1) でできてしまいます。それでも「ハッシュテーブルがあれば二分探索木はいらない😤」とならないのは、二分探索木では 範囲検索 が効率的にできるためです。

範囲検索とは、「パラメーターとして最小値と最大値を指定する。二分探索木の値のうち、最小値と最大値の間の値をすべて返却する」操作とします。両側を挟んだ範囲検索だけでなく、最小値を無限小としたり、最大値を無限大とすることで、片側の範囲検索も同じように考えることができます。

例を見ていきます。

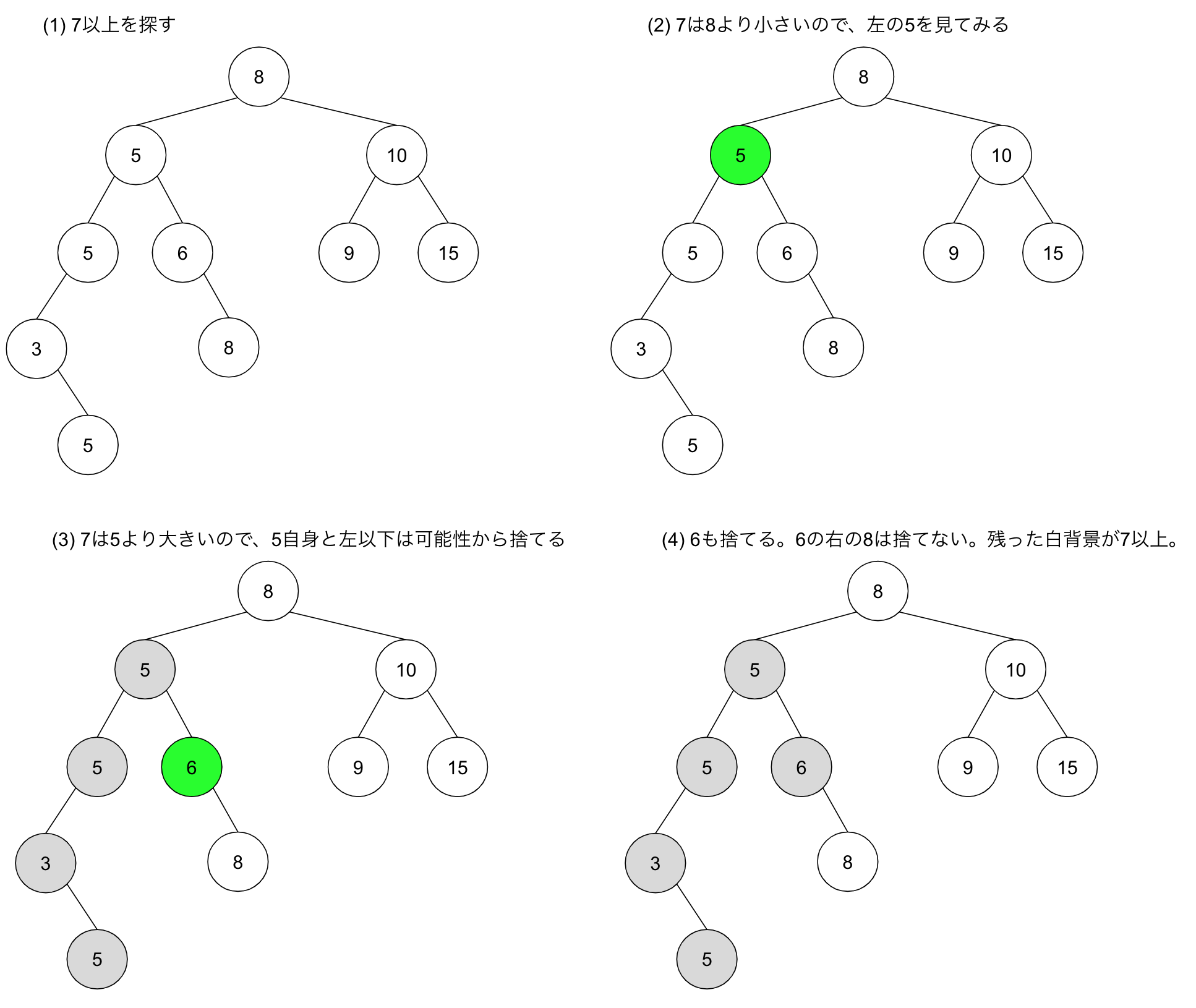
二分探索木から7以上を範囲検索

最小値を指定した範囲検索では、その最小値よりも更に小さいノードを見つけた瞬間に、そのノードの左のサブツリーは探索範囲から排除（枝刈り）できるのが肝です。検索範囲が広ければ、最大で二分探索木の要素数 n と同じ O(n) の計算量になってしまいますが、検索範囲が狭ければもっと小さい計算量で済みます（ O(h) に近づいていく）。

二分探索木のアルゴリズム: ソート

二分探索木はソートも高速です。というより、二分探索木は値の順序性を保ちながら構築していくので、元々がソート済みというわけです。

n 個の要素の列をソートするアルゴリズムは色々ありますが、大体速いもので時間計算量 O(n * log n) 程度になります（空間計算量を多く使う基数ソートなどでは O(n) も可能ですが）。一方、要素が n 個の二分探索木からソート済みの値の列を取り出すのは、 O(n) で可能です。

計算手順は単純です。二分探索木を深さ優先探索しながら、in-place orderで値を配列に追加していけばその配列はソート済みの列になっています。in-place orderとは、「左のサブツリー、親自身、右のサブツリー」の順に処理をすることであり、一般の二分木に関する処理順序のひとつです。

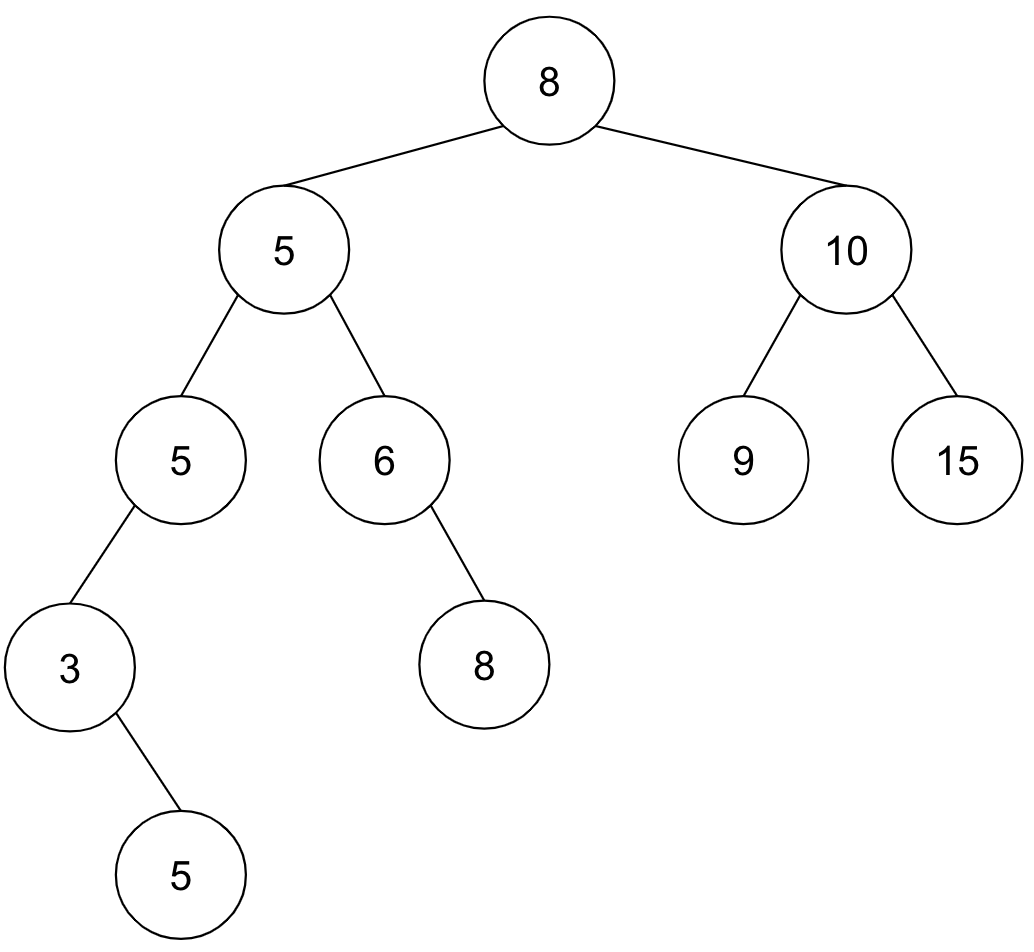
簡単な二分探索木

この二分探索の要素をin-place orderで出力していくと、 3, 5 (深さ5), 5 (深さ3), 5 (深さ2), 6, 8 (深さ4), 8 (深さ1), 9, 10, 15 と、ソート済みの列になりますね。

以下、in-place order に関する参考です。読み飛ばしても二分探索木の理解上問題ありません。

参考: in-place order, pre-order, post-order で値を出力
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
    a
   / \
  b   e
 / \
c   d

in-order (左, 親, 右 の順) : c, b, d, a, e
pre-order (親, 左, 右 の順) : a, b, c, d, e
post-order (左, 右, 親 の順) : c, d, b, e, a

それぞれ、再帰関数の書き方を考えるとわかりやすい。

in-order:
  rec(parent) {
    rec(parent.left)
    do(parent)
    rec(parent.right)
  }

pre-order:
  rec(parent) {
    do(parent)
    rec(parent.left)
    rec(parent.right)
  }

post-order:
  rec(parent) {
    rec(parent.left)
    rec(parent.right)
    do(parent)
  }

二分探索木のアルゴリズム: 値の追加

ここまでは、既に構築された二分探索木を読むアルゴリズムを見てきました。ここでは、二分探索木に値を追加していくことを考えます。

二分探索木の制約をもう一度見てみましょう。

  1. ノードは大小が定義できる値を持つ。
  2. あるノードの左側の子孫ノードは、そのノードの値 以下 の値を持つ。
  3. あるノードの右側の子孫ノードは、そのノードの値 以上 の値を持つ。

これを満たすような二分木は、値の集合が同じでも複数種類存在することも見てきました。

同一の値の集合から異なる二分探索木が構成できる

挿入方法も色々なバリエーションが考えられ、これを工夫すると深さのバランスの取れた平衡二分探索木を構成することができます。そのアルゴリズムは次回に回し、ここでは以下のようなシンプルな挿入アルゴリズムを考えます。

  1. 必ずリーフ要素として追加する。
  2. 二分探索木の制約を守るために、検索アルゴリズムと同じ考え方で、挿入すべきリーフを深さ優先探索していく。

ここまで使ってきている二分探索木に、 7 を追加することを考えます。

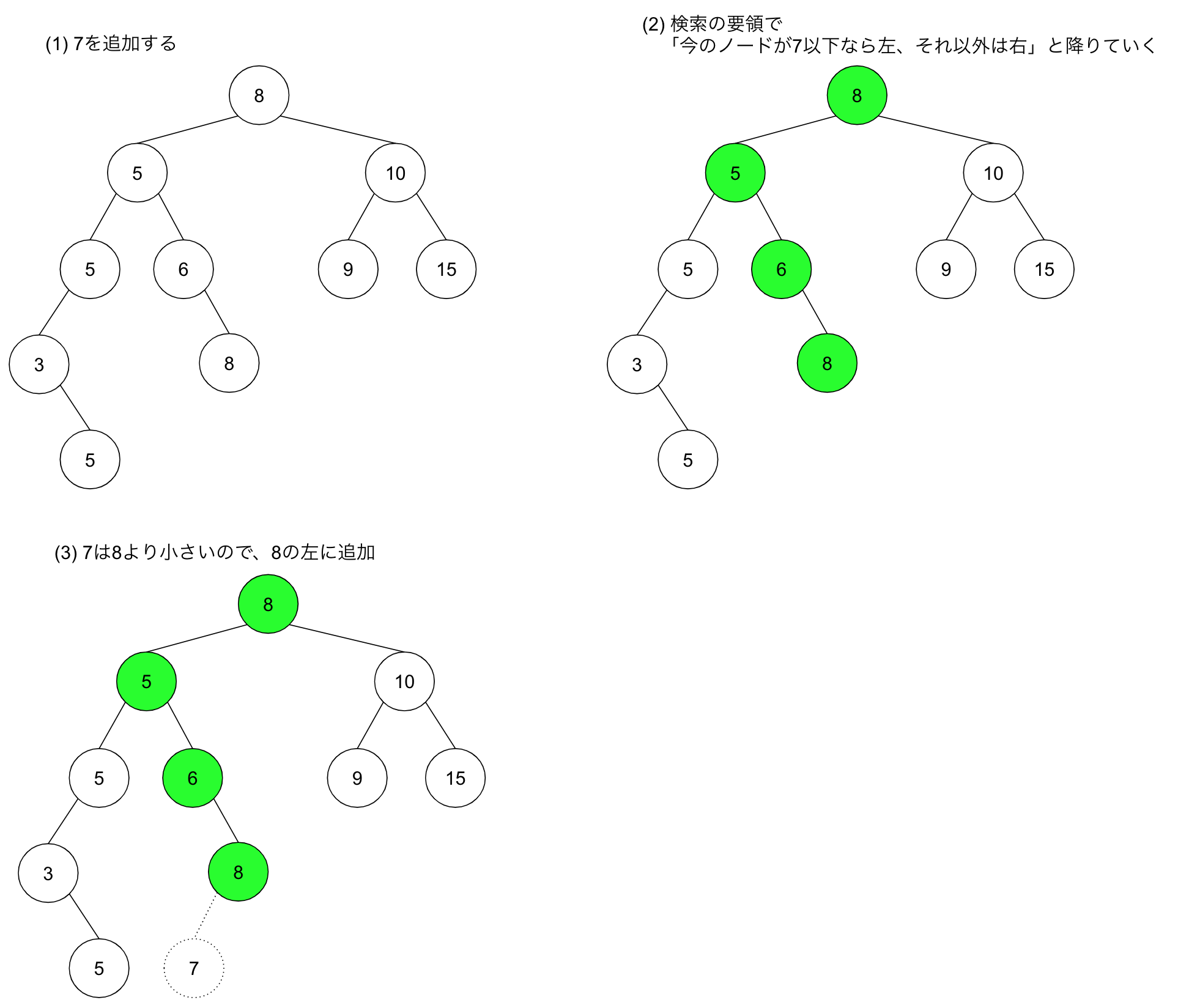
二分探索木に7を追加

追加後の二分探索木が大小の制約を満たしていることを確認してみてください。

Rustで定義する二分探索木

データ構造とコンストラクタ

ここまでで二分探索木のデータ構造とアルゴリズムを一気に見てきました。これらをRustで実装してみましょう。まずはデータ構造から。

二分探索木のデータ構造は、二分木のデータ構造とほとんど差がありません。二分木よりも厳しい制約は「値が小さければ左、大きければ右」という値レベルのものなので、型レベルの違いではないからです。とはいえ、その値レベルの違いのルールを破らないようにするため、構築に関して縛りを入れるべきです。

第1回の二分木の構築 では、 enum BinaryTree::Node の val, left, right を直接埋めていました。これだと、 left.val > val になるような構築もできてしまい、二分探索木としては困ってしまいます。

Rustのenumは、enum自体がpublicならば全要素publicになってしまうので、structと組み合わせて「何でもできるコンストラクタ」を隠蔽し、空の二分探索木を作る new() コンストラクタを提供します。

二分探索木のデータ構造
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/// 二分探索木。
/// あるノードと等しい値は、必ず左側の子ノード以下に入ることとする。
///
///          8
///       __/ \__
///      /       \
///     5        10
///    / \      /  \
///   5   6    9   15
///  /     \
/// 3       8
///  \
///   5
///
#[derive(Debug, PartialEq, Eq)]
pub struct BinarySearchTree<T: Ord>(
    // private に実体を持つ。enumを直接使った構築はできない。
    BinarySearchTreeInner<T>,
);

/// 実体。二分木と同じフィールド。
#[derive(Debug, PartialEq, Eq)]
enum BinarySearchTreeInner<T: Ord> {
    Nil,
    Node {
        val: T,
        left: Box<Self>,
        right: Box<Self>,
    },
}

impl<T: Ord> BinarySearchTree<T> {
    /// 空の二分探索木をつくる。
    pub fn new() -> Self {
        Self(BinarySearchTreeInner::Nil)
    }
}

二分探索木と異なり、ノードの値が任意の型ではなく、 Ord （順序付き）であることを制約として持つ点に注意してください。

要素の追加

値を追加するメソッド add() を定義します。

要素の追加
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
impl<T: Ord> BinarySearchTree<T> {
    /// 二分探索木に val を追加する。
    /// val は二分探索木に組み込まれる形で move される。
    pub fn add(&mut self, val: T) {
        // val を配置すべきNilを探索。
        let nil = Self::find_nil_to_add(&mut self.0, &val);

        // ノード値が val であるようなリーフを作り、Nilを置き換える。
        *nil = BinarySearchTreeInner::Node {
            val,
            left: Box::new(BinarySearchTreeInner::Nil),
            right: Box::new(BinarySearchTreeInner::Nil),
        }
    }

    /// val を二分探索木に追加する場合に、val と交換すべき箇所の Nil を、深さ優先探索で探す、再帰関数。
    ///
    /// 上図の二分木の例だと、
    /// - val == 1 の場合: `3` の左の Nil
    /// - val == 5 の場合: リーフの `5` の左の Nil
    /// - val == 16 の場合: `15` の右の Nil
    ///
    /// 生存期間パラメータの解説:
    /// - 't : 二分探索木自体の生存期間。 cur_node (現在探索中のノード) も、置き換えるべき Nil も、二分探索木自体の生存期と一致している。
    /// - 'v : 追加する要素の生存期間
    fn find_nil_to_add<'t, 'v>(
        cur_node: &'t mut BinarySearchTreeInner<T>,
        val: &'v T,
    ) -> &'t mut BinarySearchTreeInner<T> {
        match cur_node {
            // Nil まで到達したら、それが val と置き換えるべき Nil。
            BinarySearchTreeInner::Nil => cur_node,

            BinarySearchTreeInner::Node {
                val: cur_v,
                left,
                right,
            } => {
                if val <= cur_v {
                    // 探索中のノード値以下の値を追加したいなら、左に降りる
                    Self::find_nil_to_add(left, &val)
                } else {
                    Self::find_nil_to_add(right, &val)
                }
            }
        }
    }
}

private な再帰関数 find_nil_to_add() が登場します。これは意味合い的には add() の中の内部関数で十分なのですが、型パラメーター T を内部関数に持ってくることができないため、 BinarySearchTree のメソッドとして定義しています。
find_nil_to_add() の生存期間パラメータは少々難しいポイントです。明示的に指定しなければ、 cur_node , val , 返り値の参照のすべてが同一の生存期間となります。これは制約としては少々厳しすぎます。 val はまだ二分探索木に取り込まれていない外からの値の参照なので、これの生存期間は二分探索木の生存期間と分けて定義してあげるべきでしょう。そうしなければ、

add() を呼び出す
1
2
3
4
{
    let mut bst1 = BinarySearchTree::new();
    bst1.add(1);  // 1 リテラルの生存期間は、 {} ブロック内よりも短い
}

このコードがコンパイルエラーとなります。

使い方を示すためにも、テストコードを記載します。

add() の単体テスト
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#[test]
fn add_in_same_order() {
    use BinarySearchTree;

    let mut bst1 = BinarySearchTree::new();
    bst1.add(1);
    bst1.add(2);

    let mut bst2 = BinarySearchTree::new();
    bst2.add(1);
    bst2.add(2);

    assert_eq!(bst1, bst2);
}

#[test]
fn add_in_different_order1() {
    use BinarySearchTree;

    let mut bst1 = BinarySearchTree::new();
    bst1.add(1);
    bst1.add(2);

    let mut bst2 = BinarySearchTree::new();
    bst2.add(2);
    bst2.add(1);

    assert_ne!(bst1, bst2);
}

#[test]
fn add_in_different_order2() {
    use BinarySearchTree;

    let mut bst1 = BinarySearchTree::new();
    bst1.add(8);
    bst1.add(5);
    bst1.add(10);
    bst1.add(5);
    bst1.add(3);
    bst1.add(5);
    bst1.add(6);
    bst1.add(8);
    bst1.add(9);
    bst1.add(15);

    let mut bst2 = BinarySearchTree::new();
    bst2.add(8);
    bst2.add(10);
    bst2.add(5);
    bst2.add(15);
    bst2.add(9);
    bst2.add(6);
    bst2.add(5);
    bst2.add(8);
    bst2.add(3);
    bst2.add(5);

    assert_eq!(bst1, bst2);
}

同じ要素の集合を異なる順番で追加したとき、最終的な二分探索木が同じ構造になることも違う構造になることもあります。紙に書きながら add() のアルゴリズムをたどれば理解は難しくないはずです。

一致検索

一致検索はとても素直な再帰で書けます。

一致検索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
impl<T: Ord> BinarySearchTree<T> {
    /// 二分探索木に val が1つ以上含まれているかを返す。
    pub fn contains(&self, val: &T) -> bool {
        Self::contains_inner(&self.0, &val)
    }

    fn contains_inner(cur_node: &BinarySearchTreeInner<T>, val: &T) -> bool {
        match cur_node {
            BinarySearchTreeInner::Nil => false, // たどってきたpathには val がなかった

            BinarySearchTreeInner::Node {
                val: cur_v,
                left,
                right,
            } => {
                if cur_v == val {
                    // val を見つけたら、リーフまで到達していなくても、これ以上の再起をやめてtrueを返す
                    true
                } else {
                    // 左か右のどちらかに val があるかどうか
                    Self::contains_inner(left, val) || Self::contains_inner(right, val)
                }
            }
        }
    }
}

#[test]
fn contains() {
    let mut bst = BinarySearchTree::new();
    bst.add(8);
    bst.add(5);
    bst.add(10);
    bst.add(5);
    bst.add(3);
    bst.add(5);
    bst.add(6);
    bst.add(8);
    bst.add(9);
    bst.add(15);

    assert_eq!(bst.contains(&0), false);
    assert_eq!(bst.contains(&5), true);
    assert_eq!(bst.contains(&10), true);
    assert_eq!(bst.contains(&9), true);
    assert_eq!(bst.contains(&15), true);
    assert_eq!(bst.contains(&16), false);
}

ソート

in-place order で Vec に値を詰めていくだけです。本当は Vec よりもイテレーターを返すほうがメモリ確保を必要なときまで遅延できるのでベターですが、ここでは二分探索木にフォーカスするために Vec を返却します。

ソート
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
impl<T: Ord> BinarySearchTree<T> {
    pub fn get_all_sorted(&self) -> Vec<&T> {
        let mut ret = Vec::<&T>::new();
        Self::get_all_sorted_inner(&self.0, &mut ret);
        ret
    }

    /// in-place order で ret にノード値を追加していく
    fn get_all_sorted_inner<'t, 'a>(
        cur_node: &'t BinarySearchTreeInner<T>,
        ret: &'a mut Vec<&'t T>,
    ) {
        match cur_node {
            BinarySearchTreeInner::Nil => {}
            BinarySearchTreeInner::Node { val, left, right } => {
                Self::get_all_sorted_inner(left, ret);
                ret.push(val);
                Self::get_all_sorted_inner(right, ret);
            }
        }
    }
}

#[test]
fn get_all_sorted() {
    let mut bst = BinarySearchTree::new();
    bst.add(8);
    bst.add(5);
    bst.add(10);
    bst.add(5);
    bst.add(3);
    bst.add(5);
    bst.add(6);
    bst.add(8);
    bst.add(9);
    bst.add(15);

    assert_eq!(
        bst.get_all_sorted(),
        vec![&3, &5, &5, &5, &6, &8, &8, &9, &10, &15]
    );
}

範囲検索

範囲検索も、ソートと同じく in-place order で再帰処理をすれば、自然にソート済みの検索結果が得られます。「左の子以下は今見ているノードの値以下なので、探している val は絶対にない」のように枝刈りしていることに着目してください。

範囲検索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
impl<T: Ord> BinarySearchTree<T> {
    pub fn get_range_sorted(&self, min: &T, max: &T) -> Vec<&T> {
        let mut ret = Vec::<&T>::new();
        Self::get_range_sorted_inner(&self.0, min, max, &mut ret);
        ret
    }

    /// in-place order で [min, max] の範囲のノード値を検索し、 ret に追加していく
    fn get_range_sorted_inner<'t, 'a>(
        cur_node: &'t BinarySearchTreeInner<T>,
        min: &T,
        max: &T,
        ret: &'a mut Vec<&'t T>,
    ) {
        match cur_node {
            BinarySearchTreeInner::Nil => {}
            BinarySearchTreeInner::Node { val, left, right } => {
                if val >= min {
                    // cur_node の値が最小値以上なら、まだ左の子ノード以下に最小値以上のノード値があり得るので、探索する。
                    Self::get_range_sorted_inner(left, min, max, ret);
                }
                if min <= val && val <= max {
                    ret.push(val);
                }
                if val < max {
                    // cur_node の値が最大値より小さければ、まだ右の子ノード以下に最大値以下のノード値があり得るので、探索する。
                    Self::get_range_sorted_inner(right, min, max, ret);
                }
            }
        }
    }
}

#[test]
fn get_range_sorted() {
    let mut bst = BinarySearchTree::new();
    bst.add(8);
    bst.add(5);
    bst.add(10);
    bst.add(5);
    bst.add(3);
    bst.add(5);
    bst.add(6);
    bst.add(8);
    bst.add(9);
    bst.add(15);

    assert_eq!(
        bst.get_range_sorted(&3, &15),
        vec![&3, &5, &5, &5, &6, &8, &8, &9, &10, &15]
    );
    assert_eq!(
        bst.get_range_sorted(&5, &15),
        vec![&5, &5, &5, &6, &8, &8, &9, &10, &15]
    );
    assert_eq!(
        bst.get_range_sorted(&5, &14),
        vec![&5, &5, &5, &6, &8, &8, &9, &10]
    );
    assert_eq!(bst.get_range_sorted(&5, &5), vec![&5, &5, &5]);
}

応用編: LeetCode の問題を解いてみる

説明した操作やアルゴリズムで実際の問題が解決できることを例示するために、 LeetCode から以下の問題を取り上げます。

  • 938. Range Sum of BST
    • 二分探索木と、最小値・最大値が与えられたとき、最小値と最大値の間のノード値の総和を回答。

これは 範囲検索 した結果の Vec を足し合わせれば一発ですね。特に新しく回答関数を書いたりする必要もありません。サンプルの入出力を確かめるテストだけ書きます。

938. Range Sum of BST
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#[test]
fn leetcode_938_range_sum_of_bst() {
    //          10
    //         /  \
    //        5    15
    //       / \     \
    //      3   7     18
    let mut bst1 = BinarySearchTree::new();
    bst1.add(10);
    bst1.add(5);
    bst1.add(3);
    bst1.add(7);
    bst1.add(15);
    bst1.add(18);
    assert_eq!(bst1.get_range_sorted(&7, &15).into_iter().sum::<i32>(), 32);

    //          10
    //       __/  \__
    //      /        \
    //     5         15
    //    / \       /  \
    //   3   7     13   18
    //  /   /
    // 1   6
    let mut bst2 = BinarySearchTree::new();
    bst2.add(10);
    bst2.add(5);
    bst2.add(3);
    bst2.add(7);
    bst2.add(1);
    bst2.add(6);
    bst2.add(15);
    bst2.add(13);
    bst2.add(18);
    assert_eq!(bst2.get_range_sorted(&6, &10).into_iter().sum::<i32>(), 23);
}

終わりに

この記事ではRustで二分探索木をシンプルに定義する方法と、二分探索木の構築・追加、そして一致検索・範囲検索・ソートを紹介しました。

一致検索の説明 で指摘したように、二分探索木の強みは一致検索が O(h) （木の深さ）程度でできるだけでなく、範囲検索が O(n) （木の要素数）より小さい計算量で実現でき、もともとソート済みの構造になるので O(n) でソート済の列が得られることにあります。
ただし、ただの二分探索木の制約では、木の深さ h が最大で要素数の n になってしまいます（例: ルートに最小値、右の子ノードに次に大きい値、と小さい順に右に連ねる場合）。

次回は木の深さを小さく抑える工夫の詰まった、平衡二分探索木を紹介します。

author Sho Nakatani a.k.a. laysakura

JTCのプリンシパル・リサーチャーとして、セキュリティ・プライバシー・データ基盤に関する研究開発に従事。
CISSP/OSCP/BSCP/情報処理安全確保支援士(合格) 等の資格保有。CTF上位入賞多数。 セキュリティ関連の執筆・講演活動も行っている。
（詳細プロフィール）