“パタヘネ本” でおなじみの『コンピュータの構成と設計 第5版』の解答集です。読者は書籍を保有していることを前提として解答・解説を記載します。
訂正案などありましたら本ブログ記事のリポジトリ へPull-Requestくだされば幸いです😊

この記事3章の内容は、

• 加算と減算
• 乗算器
• 除算器
• 浮動小数点数
• SIMD

です。

各章の解答集

1. 『コンピュータの構成と設計 第5版』演習問題解答集 第1章 （執筆中）
2. 『コンピュータの構成と設計 第5版』演習問題解答集 第2章
3. 『コンピュータの構成と設計 第5版』演習問題解答集 第3章 （この記事）
4. 『コンピュータの構成と設計 第5版』演習問題解答集 第4章
5. 『コンピュータの構成と設計 第5版』演習問題解答集 第5章 （執筆中）
6. 『コンピュータの構成と設計 第5版』演習問題解答集 第6章 （執筆中）

問題・解答・解説へジャンプ

• 3.1
• 3.2
• 3.3
• 3.4
• 3.5
• 3.6
• 3.7
• 3.8
• 3.9
• 3.10
• 3.11
• 3.12
• 3.13
• 3.14
• 3.15
• 3.16
• 3.17
• 3.18
• 3.19
• 3.20
• 3.21
• 3.22
• 3.23
• 3.24
• 3.25
• 3.26 (未回答)
• 3.27
• 3.28 (未回答)
• 3.29
• 3.30
• 3.31
• 3.32
• 3.33
• 3.34
• 3.35
• 3.36
• 3.37
• 3.38 (未回答)
• 3.39 (未回答)
• 3.40 (未回答)
• 3.41
• 3.42
• 3.43
• 3.44
• 3.45
• 3.46
• 3.47

3.1

問題

符号なし16進数の5ED4－07A4はいくつか．計算の過程と，16進数の結果を示せ．

解答

$$\begin{array}{rr}& \mathtt{\text{5}}\mathtt{\text{E}}\mathtt{\text{D}}\mathtt{\text{4}}\\ -& \mathtt{\text{0}}\mathtt{\text{7}}\mathtt{\text{A}}\mathtt{\text{4}}\\ & \mathtt{\text{5}}\mathtt{\text{7}}\mathtt{\text{3}}\mathtt{\text{0}}\end{array}$$

解説

特になし

3.2

問題

符号拡張形式で格納されている符号付き16進数の5ED4－07A4はいくつか．計算の過程と，16進数の結果を示せ．

解答

32ビット整数と解釈する。符号拡張形式であってもともに正の数。
3.1と経過も変わらず、

$$\begin{array}{rr}& \mathtt{\text{5}}\mathtt{\text{E}}\mathtt{\text{D}}\mathtt{\text{4}}\\ -& \mathtt{\text{0}}\mathtt{\text{7}}\mathtt{\text{A}}\mathtt{\text{4}}\\ & \mathtt{\text{5}}\mathtt{\text{7}}\mathtt{\text{3}}\mathtt{\text{0}}\end{array}$$

解説

16ビットの符号拡張形式であっても、先頭ビットがともに0なので、全く同じ。

3.3

問題

5ED4を2進数に変換せよ．コンピュータ内で値を表現するのに，基数を16（16進数）にすると都合が良いのは，どのような点か．

解答

$010111101101{0100}_2$

16進数は、「1桁が2進数4桁に対応」という特徴を持つので、2進数との相互変換性が高く、2進数よりも少ない桁数で表現できるのが良い点。
かつ、2進数8桁が1バイトなので、16進数2桁でちょうど1バイトを表すことができる。コンピュータではバイト単位の処理が多いのでこれも利便性が高い。

解説

特になし。

3.4

問題

12ビットの符号なし８進数の4365－3412はいくつか．計算の過程と，8進数の結果を示せ．

解答

$$\begin{array}{rr}& \mathtt{\text{4}}\mathtt{\text{3}}\mathtt{\text{6}}\mathtt{\text{5}}\\ -& \mathtt{\text{3}}\mathtt{\text{4}}\mathtt{\text{1}}\mathtt{\text{2}}\\ & \mathtt{\text{0}}\mathtt{\text{7}}\mathtt{\text{5}}\mathtt{\text{3}}\end{array}$$

解説

右から3~4桁目で繰り下げが発生している点に注意。

3.5

問題

符号拡張形式で格納されている符号付き12ビットの8進数の4365－3412はいくつか．計算の過程と，8進数の結果を示せ．

解答

3.4と同様に、

$$\begin{array}{rr}& \mathtt{\text{4}}\mathtt{\text{3}}\mathtt{\text{6}}\mathtt{\text{5}}\\ -& \mathtt{\text{3}}\mathtt{\text{4}}\mathtt{\text{1}}\mathtt{\text{2}}\\ & \mathtt{\text{0}}\mathtt{\text{7}}\mathtt{\text{5}}\mathtt{\text{3}}\end{array}$$

ただし、オーバーフローが発生していることに注意。

解説

${4365}_8$ は、先頭ビットが1なので、負の数である。${3412}_8$ は先頭ビットが0なので、正の数である。
“負の数 - 正の数” の計算なので、オーバーフローが発生する可能性がある。

解答とは別の方式で検算してみる。まずは、第2項の2の補数表現 $-{3412}_8=-011100001{010}_2=100011110{110}_2={4366}_8$ と、第1項を加算する。

$$\begin{array}{rr}& \mathtt{\text{4}}\mathtt{\text{3}}\mathtt{\text{6}}\mathtt{\text{5}}\\ +& \mathtt{\text{4}}\mathtt{\text{3}}\mathtt{\text{6}}\mathtt{\text{6}}\\ & \mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{7}}\mathtt{\text{5}}\mathtt{\text{3}}\end{array}$$

先頭の桁はオーバーフローで落ちるので、 ${0753}_8$ を得る。

今度は第1項の2の補数表現 ${4365}_8=100011110{101}_2=-011100001{011}_2=-{3413}_8$ と、第1項を加算したものを符号反転する。まずは加算。

$$\begin{array}{rr}& \mathtt{\text{3}}\mathtt{\text{4}}\mathtt{\text{1}}\mathtt{\text{3}}\\ +& \mathtt{\text{3}}\mathtt{\text{4}}\mathtt{\text{1}}\mathtt{\text{2}}\\ & \mathtt{\text{7}}\mathtt{\text{0}}\mathtt{\text{2}}\mathtt{\text{5}}\end{array}$$

ここまでで、 ${4365}_8-{3412}_8=-{3413}_8-{3412}_8=-({3413}_8+{3412}_8)=-{7025}_8$ と計算できた。更に進めて、 $-{7025}_8=-111000010{101}_2=000111101{011}_2={0753}_8$ と、解答の8進数を得る。

3.6

問題

8ビットの符号なし10進整数の185と122があるとする．185－122を計算せよ．オーバフローまたはアンダフローが発生するか，それともどちらも発生しないか．

解答

${185}_{10}-{122}_{10}={63}_{10}$

オーバーフローもアンダーフローも発生しない。

解説

アンダーフローは整数演算ではなく浮動小数点演算で出てくる概念。負の整数が絡む演算で桁あふれした場合もオーバーフロー。

3.7

問題

8ビットの符号付き10進整数の185と122があるとする．185＋122を計算せよ．オーバフローまたはアンダフローが発生するか，それともどちらも発生しないか．

解答

${185}_{10}+{122}_{10}={51}_{10}$

オーバーフローもアンダーフローも発生しない。

解説

${185}_{10}$ は負の数、 ${122}_{10}$ は正の数なので、これらの加算はオーバーフローしない。

${185}_{10}$ の2の補数を $\overline{{185}_{10}}$ とすると、

$$\begin{array}{rclrc}{185}_{10}+\overline{{185}_{10}}& =& {256}_{10}\overline{{185}_{10}}& =& {256}_{10}-{185}_{10}={71}_{10}\end{array}$$

よって、 ${185}_{10}+{122}_{10}=-{71}_{10}+{122}_{10}={51}_{10}$

3.8

問題

符号拡張形式で格納されている8ビットの符号付き10進整数の185と122があるとする．185－122を計算せよ．オーバフローまたはアンダフローが発生するか，それともどちらも発生しないか．

解答

63

オーバーフローが発生している。

解説

${185}_{10}$ は負の数、 ${122}_{10}$ は正の数なので、これらの減算はオーバーフローの可能性がある。

$$\begin{array}{rcl}{185}_{10}-{122}_{10}& =& 1011{1001}_2-0111{1010}_2\\ & =& 1011{1001}_2+1000{0110}_2\\ & =& 10011{1111}_2\end{array}$$

オーバーフローしていて、 $0011{1111}_2={63}_{10}$ と評価される。
この値は、符号なし整数として ${185}_{10}-{122}_{10}$ を計算した結果と同じである。

3.9

問題

2の補数形式で格納されている8ビットの符号付き10進整数の151と214があるとする．飽和演算を用いて，151＋214を計算せよ．計算の過程と，10進数の結果を示せ．

解答

${151}_{10}+{214}_{10}=-{105}_{10}+(-{42}_{10})=-{128}_{10}$

解説

最後の式変形で飽和している。

3.10

問題

2の補数形式で格納されている8ビットの符号付き10進整数の151と214があるとする．飽和演算を用いて，151－214を計算せよ．計算の過程と，10進数の結果を示せ．

解答

${151}_{10}-{214}_{10}=-{105}_{10}-(-{42}_{10})=-{63}_{10}$

解説

特になし

3.11

問題

8ビットの符号なし整数の151と214があるとする．飽和演算を用いて，151＋214を計算せよ．計算の過程と，10進数の結果を示せ．

解答

${151}_{10}+{214}_{10}={255}_{10}$

解説

飽和している。

3.12

問題

図3.6に示されているのに似た表を使用し，図3.3に記述されているハードウエアを使用して，6ビットの符号なし8進数の整数の62と12の積を計算せよ．ステップごとに，各レジスタの内容を示せ．

解答

サイクル4のステップ1aまで計算した時点で、あとは乗数が0のビットしか残っていないので、積への加算がないことがわかる。

したがって ${62}_8$ と ${12}_8$ の積は $000111110{100}_2={764}_8$

解説

• 被乗数, 乗数ともに6ビットなので、被乗数レジスタを12ビット, 乗数レジスタを6ビット, 積レジスタを12ビットとすれば十分。

3.13

問題

図3.6に示されているのに似た表を使用し，図3.5に記述されているハードウエアを使用して，8ビットの符号なし16進数の整数の62と12の積を計算せよ．ステップごとに，各レジスタの内容を示せ．

解答

解説

前問が ${62}_8\times {12}_8$ の計算だったの対し、本文は ${62}_{16}\times {12}_{16}$ の計算であることに注意（悪意を感じる🙄）。

初期状態から計算結果を出すまでの乗数レジスタ（8ビット）、加算キャリー・積・被乗数レジスタ（17ビット）の値を下記に図示する。

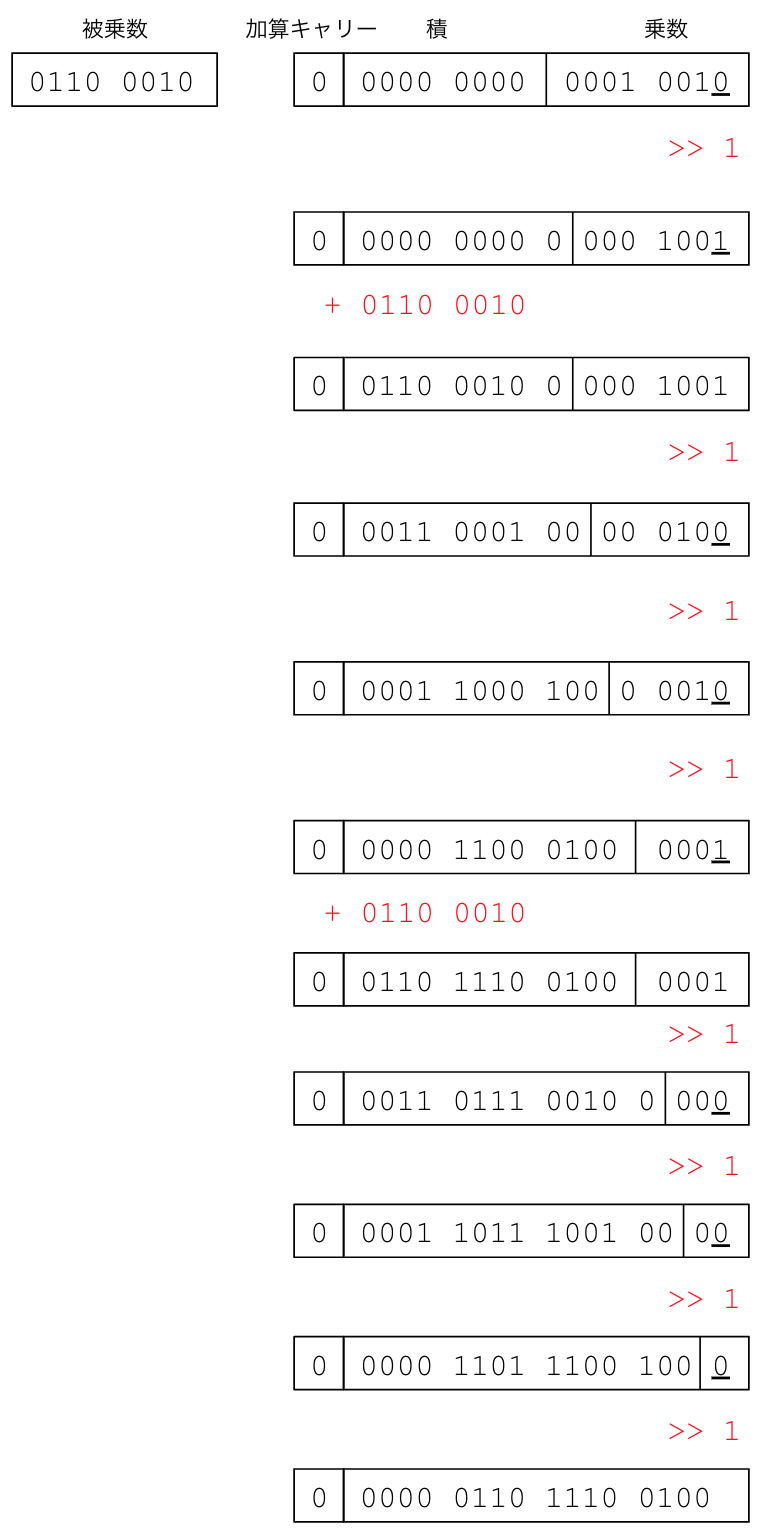
これを表形式に合わせて解答を得る。

3.14

問題

図3.3および図3.4に示されている方法に従い，整数の長さが8ビットで，各ステップの処理に4単位時間かかるとして，乗算を行うのに必要な時間を計算せよ．ステップ1においては，必ず加算が行われる，と想定する．つまり，被乗数またはゼロが加算される．また，レジスタは既に初期化されている，と想定する（乗算ループを回る回数を数えるだけでよい）．この処理をハードウエアで行う場合は，被乗数と乗数のシフトを同時に実行できる．この処理をソフトウエアで行う場合は，被乗数と乗数のシフトを順に実行しなければならない．両方の場合について，問題を解け．

解答

• 図3.3:
  • ハードウェア処理: 128単位時間
  • ソフトウェア処理: 160単位時間
• 図3.4:
  • ハードウェア処理: 160単位時間
  • ソフトウェア処理: 160単位時間

解説

• 図3.3の形式について:
  • 乗数レジスタを右シフトする1サイクルの間に下記のステップを実行する。
    • 乗数レジスタの最下位ビットの0/1を判定。
    • 積レジスタに被乗数レジスタ(最下位ビットが1のとき)または0(最下位ビットが0のとき)を加える。
    • 被乗数レジスタを左シフト。
    • 乗数レジスタを右シフト。
    • 繰り返し回数が8回に達したか判定。
  • ハードウェア処理ならば、被乗数レジスタの左シフトと乗数レジスタの右シフトが同一ステップで実行できるので、ハードウェア処理は4ステップ、ソフトウェア処理は5ステップ。
  • この処理は、8ビットなので8回繰り返される。
  • したがって、ハードウェア処理は32ステップ、ソフトウェア処理は40ステップ。
• 図3.4の形式について:
  • 乗数レジスタを右シフトする1サイクルの間に下記のステップを実行する。
    • 積・乗数レジスタの最下位ビットの0/1を判定。
    • 積・乗数レジスタに被乗数レジスタ(最下位ビットが1のとき)または0(最下位ビットが0のとき)を加える。
    • 積・乗数レジスタを右シフト。
    • 繰り返し回数が8回に達したか判定。
  • この処理は、8ビットなので8回繰り返される。
  • したがって、ハードウェア処理でもソフトウェア処理でも32ステップ。

3.15

問題

本文に記述されている方法（縦に積み上げられた31個の加算器）に従い，整数の長さが8ビットで，加算器の処理に4単位時間かかるとして，乗算を行うのに必要な時間を計算せよ．

解答

問題文に指定されていないので、乗数の各ビットに応じて

• 0ならば、0を加算器への入力値にする
• 1ならば、被乗数を加算器への入力値にする

という処理には、 $n$ 単位時間 かかるものとする。乗数31~0ビット目はそれぞれ独立に判定できるので、上記の処理を32ビット分並列に行えば $n$ 単位時間で済む。

あとは、逐次的に32ステップかけて加算器の結果を足し合わせていくので、合計で $n+32\times 4=n+128$ 単位時間を要する。

解説

特になし。

3.16

問題

図3.7に示されている方法に従い，整数の長さが8ビットで，加算器の処理に4単位時間かかるとして，乗算を行うのに必要な時間を計算せよ．

解答

3.15と同様の $n$ を導入。

加算器の適用は5ステップで済むので、 $n+5\times 4=n+20$ 単位時間を要する。

解説

特になし。

3.17

問題

本文に記述されているように，性能を向上させる1つの可能性は，実際の乗算の代わりに，シフトと加算を行うことである．たとえば，9×6＝（2×2×2＋1）×6である．したがって，6を左に3回シフトし，その結果に6を加えることにより，9×6を計算できる．シフトと加算を用いて，0x33×0x55を計算する，最善の方法を示せ．入力データは共に，8ビットの符号なし整数であるものとする．

解答

${33}_{16}\times {55}_{16}=((2^5{)}_{10}+1_{10})\times {55}_{16}={55}_{16}<<5+{55}_{16}$

解説

• 0x33 を2のべき乗にした場合、 ${33}_{16}\times {55}_{16}=((2^5{)}_{10}+1_{10})\times {55}_{16}$ なので、 ${55}_{16}<<5+{55}_{16}$ と計算できる。
• 0x55 を2のべき乗にした場合、 ${33}_{16}\times {55}_{16}={33}_{16}\times ((2^5{)}_{10}+{23}_{10}$ なので、 ${33}_{16}<<5+({33}_{16}+\dots (23\mathrm{回}))$ と計算できる。

前者のほうが加算の回数が少なくベター。

3.18

問題

図3.10に示されているのに似た表を使用し，図3.8に記述されているハードウエアを使用して，74割る21を計算せよ．ステップごとに，各レジスタの内容を示せ．入力データは共に，6ビットの符号なし整数であるものとする．

解答

したがって、商 ${000011}_2=3_{10}$、剰余 ${001011}_2=7_{10}$

解説

• 被除数が6ビット整数なので、処理サイクルは7回になる。

3.19

問題

図3.10に示されているのに似た表を使用し，図3.11に記述されているハードウエアを使用して，74割る21を計算せよ．ステップごとに，各レジスタの内容を示せ．AおよびBは6ビットの符号なし整数であるものとする．このアルゴリズムでは，図3.9に示されているのとは，少し違ったアプローチが必要である．よく考えて，1回か2回，試してみるとよいだろう．あるいは，インターネットから参考情報を検索する手もある（ヒント：図3.11に，剰余レジスタをどちらの方向にもシフトできる，と示唆されている．それを利用できる可能性がある．）．

解答

表形式は割愛し、図示する。

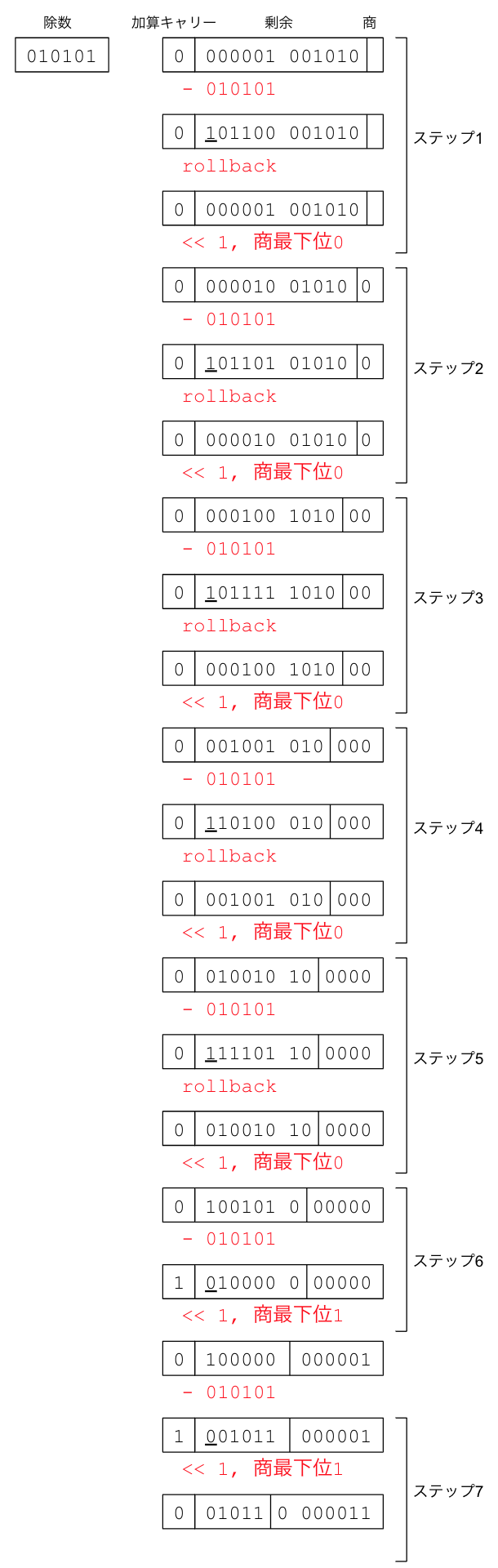
解説

• 処理サイクル数は “被除数のビット数 + 1” と設計すれば正しく計算できる。
• 除数レジスタを6ビット、剰余・商レジスタを12ビットとする（加算キャリー合わせて12ビット）。
• 初期値は、 “剰余・商” のレジスタに除数（左を0パディング）を格納。

3.20

問題

ビット・パターン0×0C000000が2の補数の整数であるならば，10進数では何を表すか．符号なしの整数であったならば，どうか．

解答

${201326592}_{10}$

解説

• 32ビット整数だと仮定する。最上位ビットが0なので、符号付きでも符号なしでも同じ正の値を指す。

3.21

問題

ビット・パターン0×0C000000を命令レジスタに入れたならば，MIPSのどの命令が実行されるか．

解答

jal 0

解説

${0\mathrm{C}000000}_{16}=0000110000000000000000000000{0000}_2$

• opcode部分の上位6ビットが $3_{16}$ なので、 jal (J形式) である。
• J形式は下位26ビットがアドレス値を指す。今回は0番地。
  • 図2.13によると、0番地はテキストセグメントの範囲外であるので、CPUのメモリ保護機構でメモリアクセスエラーになると思われる。

3.22

問題

ビット・パターン0×0C000000が浮動小数点数であるならば，10進数では何を表すか．IEEE754規格に従え．

解答

$1\times 2^{-103}$

解説

${0\mathrm{C}000000}_{16}=0000110000000000000000000000{0000}_2$

• 最初の1ビット 0 は符号。正の数。
• 次の8ビット 0001 1000 は指数部。実際の指数部の値値は、バイアス -127 を考慮して、 $(2^{{00011000}_2-{127}_{10}}{)}_{10}=(2^{-103}{)}_{10}$ 。
• 最後の23ビット 00...0 は仮数部。ただし、先頭の 1. は勝手についているとみなすので、実際の仮数部の値は ${1.00000000000000000000000}_2=1_{10}$ 。
• 以上より、 $1\times 2^{-103}$ 。

3.23

問題

IEEE754の単精度形式であるとして，10進数63.25を2進数で表現せよ．

解答

0　10000100　11111010 00000000 0000000

解説

• 2進数に変換して ${63.25}_{10}=(111111.01{)}_2$ 。
  • ${0.25}_{10}=(\frac{1}{4}{)}_{10}={0.01}_2$
• 正規化して、 $(1.1111101\times 2^5{)}_2$ 。
• バイアスを考慮して、 $(1.1111101\times 2^{132-127}{)}_2=(1.1111101\times 2^{{10000100}_2-{127}_{10}}{)}_2$ 。
• 以上より、符号は 0, 指数部は 10000100, 仮数部は（最初の 1. は不要で） 11111010 00000000 0000000

3.24

問題

IEEE754の倍精度形式であるとして，10進数63.25を2進数で表現せよ．

解答

0　100 0000 0100　11111010 00000000 00000000 00000000 00000000 00000000 0000

解説

• 倍精度が単精度と異なるのは、以下の点。
  • 指数部: 11ビットに拡張され、バイアスは1023。
  • 仮数部: 52ビットに拡張。
• 指数部について、 $2^5=2^{1028-1023}=2^{1000000{0100}_2-1023}$ なので、指数部の値は 100 0000 0100 。
• 仮数部については、単精度のものの下位ビットにゼロが多く連なるだけ。

3.25

問題

IBMの単精度形式（基数は2でなくて16，指数部は7ビット）で格納されているとして，10進数63.25を2進数で表現せよ．

解答

0　100 0100　11111101 00000000 00000000

解説

IBM単精度形式の符号化に関する情報は本書には不足しているので、 http://www.vision.is.tohoku.ac.jp/files/1814/9359/7662/3rd.pdf を参照する。

$$(-1{)}^{\mathrm{符}\mathrm{号}(1bit)}\times {16}^{\mathrm{指}\mathrm{数}\mathrm{部}(7bit)-64}\times \mathrm{仮}\mathrm{数}\mathrm{部}(24bit,1\mathrm{以}\mathrm{下})$$

という符号化らしい。

• 正の数なので符号は 0 。
• 1以下の仮数部を得るように正規化して、 ${63.25}_{10}=(0.11111101\times 2^6{)}_2$ 。
• +64 のバイアスを考慮して、 $(0.11111101\times 2^{70-64}=0.11111101\times 2^{{1000100}_2-6}$ なので、指数部の値は 100 0100 。
• 仮数部の値は 11111101 00000000 00000000 。

3.26 (未回答)

問題

DECのPDP-8で採用されたのと同様の形式（左側の12ビットは2の補数として格納される指数，右側の24ビットは2の補数として格納される仮数）を用いて，－1.5625×10－1を表すビット・パターンを示せ．暗黙の1は用いない．IEEE754規格の単精度および倍精度と比べて，この36ビット・パターンの範囲と精度について述べよ．

3.27

問題

IEEE 754-2008規格には，長さがたった16ビットの半精度がある．左端のビットはやはり符号ビットであり，指数部は長さが5ビットで15のゲタを履いており，仮数部の長さは10ビットである．暗黙の1を用いる．excess-16形式で指数を格納するこの形式を用いて，－1.5625×10－1を表すビット・パターンを示せ．IEEE754規格の単精度と比べて，この16ビットの浮動小数点形式の範囲と精度について述べよ．

解答

1　01100　01 00000000

IEEE754の単精度形式と比較して、表せる範囲は絶対値として $2^{-113}$ 倍小さく、精度は 2^{-112} 倍劣る。

解説

ビットパターンを考える。

• 負の数なので符号ビットは1。
• 絶対値を2進数で正規化して、 ${0.15625}_{10}={0.00101}_2=1.01\times 2^{-3}$
  • ${0.15625}_{10}=0\times \frac{1}{2}+0\times \frac{1}{4}+1\times \frac{1}{8}+0\times \frac{1}{16}+\frac{1}{32}={0.00101}_2$
• バイアスを考慮し、 $1.01\times 2^{12-15}=1.01\times 2^{{01100}_2-16}$ なので、指数部の値は 01100
• 暗黙の1があるので、仮数部の値は 01 00000000

範囲を考える。

• IEEE 754 の単精度浮動小数点数と同様に、指数部が全ビット0または1の数は特別な数として予約されている。有効な指数部の値は $[{00001}_2,{11110}_2]=[1_{10},{30}_{10}]$ 。バイアスを考慮し、 $[-{14}_{10},{15}_{10}]$ 。
• 仮数部で表現できる最大値は、暗黙の1も考慮し、 $(1.11\dots (\mathrm{小}\mathrm{数}\mathrm{点}\mathrm{以}\mathrm{下}23\mathrm{桁}){)}_2$ 。約2と言ってよい。
• したがって、表せる範囲は $(-2\times 2^{15},2\times 2^{15})$ 。
• IEEE 754 の単精度浮動小数点数の表せる範囲は $(-2\times 2^{128},2\times 2^{128})$ なので、絶対値にして $\frac{2^{128}}{2^{15}}=2^{113}$ 倍大きな数値が扱える。

精度を考える。

• 指数部の最小値が-14なので、 $2^{-14}$ 刻みの値を表現できる。
• IEEE 754 の単精度浮動小数点数の指数部の最小値は-126なので、 $2^{-126}$ 刻みの値を表現できる。比を取ると $\frac{2^{-14}}{2^{-126}}=2^{112}$ 。

3.28 (未回答)

問題

Hewlett-Packard 2114，2115，2116で使用された形式では，左端16ビットが2の補数として格納される仮数，その後の16ビットのうちの左半分が仮数の拡張部（仮数は全部で24ビットとなる），右半分の8ビットが指数である．ところが，ひとひねり加えられていて，指数は符合付き絶対値形式で格納され，符号ビットは右端に配置された．この形式を用いて，－1.5625×10－1を表すビット・パターンを示せ．暗黙の1は用いない．IEEE754規格の単精度と比べて，この32ビット・パターンの範囲と精度について述べよ．

3.29

問題

$2.6125\times {10}^1$ と $4.150390625\times {10}^{-1}$ との和を手作業で計算せよ．ただし，2つのデータは，問題3.27で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．

解答

• 10のべき乗部分が残っていると2進数に変換するときに邪魔なのでなくす。
  • $2.6125\times {10}^1=26.125$
  • $4.150390625\times {10}^{-1}=0.4150390625$
• 2進数に変換する。
  • $26.125={11010.001}_2$
  • $0.4150390625={0.0110101001}_2$
    • 10進小数を手計算で2進小数に変換するアルゴリズムは https://mathwords.net/syosuu2sin など参照。
• 正規化する。
  • ${11010.001}_2=1.1010001\times 2^4$
  • ${0.0110101001}_2=1.10101001\times 2^{-1}$
• 加算するため、大きい方の指数に小さい方を合わせる。
  • $1.1010001\times 2^4$
  • ${0.00000110101001}_2\times 2^4$
• IEEE 754 の16半精度浮動小数点数は、仮数部が10ビットなので、後者の数値は桁落ちして 0000011010 101 。ただし、11ビット目はガード桁。12ビット目は丸め桁。13ビット目はスティッキービット（元の13ビット目は0, 14ビット目は1だったので、1が立つ）。
• 仮数部を筆算する。

$$\begin{array}{rr}& \mathtt{\text{1}}\mathtt{\text{.}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\\ +& \mathtt{\text{0}}\mathtt{\text{.}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\\ & \mathtt{\text{1}}\mathtt{\text{.}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\mathtt{\text{0}}\mathtt{\text{1}}\end{array}$$

• 丸めを計算する。ulp (unit in the last place) は、小数点以下10桁目の 0 。それよりも小さい桁は 101 なので、 $1\times \frac{1}{2}+0\times \frac{1}{4}+1\times \frac{1}{8}=\frac{5}{8}\mathrm{u}\mathrm{l}\mathrm{p}$ 。0.5 ulp よりも大きいので、小数点以下10桁目は桁上げして 1 となる。
• 以上より、和は $1.1010100011\times 2^4$ 。

解説

スティッキービットがなければ、ガード桁と丸め桁で $\frac{1}{2}\mathrm{u}\mathrm{l}\mathrm{p}$ となるので、 “最も近い偶数への丸め” が発動し、小数点以下10桁目は 0 のままになっていた。

3.30

問題

$-8.0546875\times {10}^0$ と $1.79931640625\times {10}^{-1}$ との積を手作業で計算せよ．ただし，2つのデータは，問題3.27で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．ただし，問題3.12から3.14で説明した方法を使用する代わりに，本文中の例で示したように，人が読める形式の乗算を行ってよい．オーバフローまたはアンダフローが発生するかどうかを示せ．答えを，問題3.27で説明した16ビットの浮動小数点形式と，10進数の両方で示せ．結果はどれほど正確か．電卓を使って乗算を行った場合と比べるとどうか．

解答

• 符号は片方が負でもう片方が正なので、積の符号は負になる。

• 10のべき乗部分が残っていると2進数に変換するときに邪魔なのでなくす。

  • $8.0546875\times {10}^0=8.0546875$
  • $1.79931640625\times {10}^{-1}=0.179931640625$

• 2進数に変換する。

  • $8.0546875={1000.0000111}_2$
  • $0.179931640625={0.001011100001}_2$

• 正規化する。

  • $1000.0000111=1.0000000111\times 2^3$
  • $0.001011100001=1.011100001\times 2^{-3}$

• 積の指数部は $2^3\times 2^{-3}=2^0$ 。

• 仮数部はともに10ビットに収まる。

• 仮数部の積を筆算する。

  1 2 3 4 5 6 7 8 9 10

  1.0000000111 x 1.011100001 ---------------------- 10 000000111 1000000 0111 10000000 111 100000001 11 10000000111 ---------------------- 10111001100 000100111

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまで削ると、結果は 1.0111001100 001 となる。（スティッキービットは、13ビット目以降の 0100111 に1つ以上1が立っているので1となる。）

• ガード桁以降は $\frac{1}{8}\mathrm{u}\mathrm{l}\mathrm{p}$ なので切り捨てられ、最終ビットは0のまま。

• 以上より、積は $-1.0111001100\times 2^0$ 。

• 指数部は、バイアスを考慮して $2^0=2^{15-15}=2^{{01111}_2-15}$ なので、 01111 と符号化される。

• 全体を符号化して、 1　01111　0111001100 。

• 10進数で表すと $-{1.0111001010}_2=-(1+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{128}+\frac{1}{256})=-{1.44921875}_{10}$

• 電卓で計算すると $8.0546875\times 0.179931640625=1.4492931365966797$ 。有効数字5桁の範囲で一致。

解説

特になし。

3.31

問題

$8.625\times {10}^1$ 割る $-4.875\times {10}^0$ を手作業で計算せよ．答えを得るのに必要なすべてのステップを示せ．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，必要があればそれらを使用するものとする．最終的な答えを，問題3.27で説明した16ビットの浮動小数点形式と，10進数の両方で示せ．また，10進数の答えを，電卓を使った場合の答えと比較せよ．

入力・計算過程を保持する形式の指定がないが、IEEE 754半精度浮動小数点数を使うものとする。

解答

• 符号は片方が負でもう片方が正なので、商の符号は負になる。

• 10のべき乗部分が残っていると2進数に変換するときに邪魔なのでなくす。

  • $8.625\times {10}^1=86.25$
  • $4.875\times {10}^0=4.875$

• 2進数に変換する。

  • $86.25={1010110.01}_2$
  • $4.875={100.111}_2$

• 正規化する。

  • $1010110.01=1.01011001\times 2^6$
  • $100.111=1.00111\times 2^2$

• 商の指数部は $\frac{2^6}{2^2}=2^4$

• 仮数部はともに10ビットに収まる。

• 仮数部の商を筆算する。予め、除数の $1.00111$ を整数化するため、被除数も含めて小数点を5個ずらす(左に5シフト)。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  1.000110110000... ----------- 100111 ) 101011.001 - 100111 -------- 100 0010 - 10 0111 ---------- 1 10110 - 1 00111 --------- 111100 - 100111 -------- 101010 - 100111 -------- 110000

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまでを取ると、結果は 1.0001101100 001 となる。（スティッキービットは、13ビット目以降にも1が続くので1となる。）

• ガード桁以降は $\frac{1}{8}\mathrm{u}\mathrm{l}\mathrm{p}$ なので切り捨てられ、最終ビットは0のまま。

• 以上より、商は $-1.0001101100\times 2^4$ 。

• 指数部は、バイアスを考慮して $2^4=2^{19-15}=2^{{10011}_2-15}$ なので、 10011 と符号化される。

• 全体を符号化して、 1　10011　0001101100 。

• 10進数で表すと、 $-1.0001101100\times 2^4=-10001.101100=-({17}_{10}+\frac{1}{2}+\frac{1}{8}+\frac{1}{16})=-17.6875)$ 。

• 電卓で計算すると、 $8.625\times {10}^1/(-4.875\times {10}^0)=-17.692307692307693$ 。有効数字3桁の範囲で一致。

解説

特になし。

3.32

問題

$(3.984375\times {10}^{-1}+3.4375\times {10}^{-1})+1.771\times {10}^3$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

解答

• 10のべき乗部分が残っていると2進数に変換するときに邪魔なのでなくす。

  • $3.984375\times {10}^{-1}=0.3984375$
  • $3.4375\times {10}^{-1}=0.34375$
  • $1.771\times {10}^3=1771$

• 2進数に変換する。

  • $0.3984375={0.0110011}_2$
  • $0.34375={0.01011}_2$
  • $1771={11011101011}_2$

• 正規化する。

  • $0.0110011=1.10011\times 2^{-2}$
  • $0.01011=1.011\times 2^{-2}$
  • $11011101011=1.1011101011\times 2^{10}$

• まずは $3.984375\times {10}^{-1}+3.4375\times {10}^{-1}$ の計算。指数が既に揃っているので、仮数部の筆算をする。

  1 2 3 4

  1.10011 + 1.011 --------- 10.11111

• 指数部も考慮し、正規化をして、 $3.984375\times {10}^{-1}+3.4375\times {10}^{-1}={10.11111}_2\times 2^{-2}=1.011111\times 2^{-1}$ 。

• 次に、この結果と $1.771\times {10}^3$ の和を取る。大きい方に指数を合わせて、 $(3.984375\times {10}^{-1}+3.4375\times {10}^{-1})+1.771\times {10}^3={1.011111}_2\times 2^{-1}+{1.1011101011}_2\times 2^{10}=(0.000000000001011111+1.1011101011)\times 2^{10}$

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまで削ると、 $(0.0000000000011+1.1011101011)\times 2^{10}$

• 筆算する。

  1 2 3 4

  0.0000000000 011 + 1.1011101011 ------------------ 1.1011101011 011

• ガード桁以降は $\frac{1}{4}+\frac{1}{8}=\frac{3}{8}\mathrm{u}\mathrm{l}\mathrm{p}$ なので切り捨てられ、最終ビットは1のまま。

• 以上より、計算結果は $1.1011101011\times 2^{10}=(2^0+2^{-1}+2^{-3}+2^{-4}+2^{-5}+2^{-7}+2^{-9}+2^{-10})\times 2^{10}=2^{10}+2^9+2^7+2^6+2^5+2^3+2^1+2^0={1771}_{10}$

• 指数部は、バイアスを考慮して $2^{10}=2^{25-15}=2^{{11001}_2-15}$ なので、 11001 と符号化される。

IEEE 754半精度浮動小数点数形式: 0　11001　1011101011
10進数: 1771

解説

結果を見ると、IEEE 754半精度浮動小数点数形式も10進数表記も $1.771\times {10}^3$ の項と一致。正の数同士の浮動小数点の和は、最も大きな値とそれ以外の値の指数部分が離れていると、それ以外の値の寄与が小さくなる。

3.33

問題

$3.984375\times {10}^{-1}+(3.4375\times {10}^{-1}+1.771\times {10}^3)$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

解答

• 3.32と同様に正規化して、

  • $3.984375\times {10}^{-1}={1.10011}_2\times 2^{-2}$
  • $3.4375\times {10}^{-1}={1.011}_2\times 2^{-2}$
  • $1.771\times {10}^3={1.1011101011}_2\times 2^{10}$

• まずは $3.4375\times {10}^{-1}+1.771\times {10}^3={1.011}_2\times 2^{-2}+{1.1011101011}_2\times 2^{10}$ の計算。大きい方に指数を合わせて、 $(0.000000000001011+1.1011101011)\times 2^{10}$

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまで削ると、 $(0.0000000000011+1.1011101011)\times 2^{10}$

• 仮数部の筆算をする。

  1 2 3 4

  0.0000000000 011 + 1.1011101011 ------------------ 1.1011101011 011

• 計算途中なので、ガード桁、丸め桁、スティッキービットは保持できる。指数部も合わせた結果は $1.1011101011011\times 2^{10}$

• この値を $3.984375\times {10}^{-1}={1.10011}_2\times 2^{-2}$ と加える。大きい方に指数を合わせて、 ${1.10011}_2\times 2^{-2}+1.1011101011011\times 2^{10}=(0.00000000000110011+1.1011101011011)\times 2^{10}$

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまで削ると、 $(0.0000000000011+1.1011101011011)\times 2^{10}$

• 仮数部の筆算をする。

  1 2 3 4

  0.0000000000 011 + 1.1011101011 011 ------------------ 1.1011101011 110

• ガード桁以降は $\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\mathrm{u}\mathrm{l}\mathrm{p}$ なので、最終ビットは切り上げられる。したがってこの和の結果は $1.1011101100$ となる。

• 以上より、計算結果は $1.1011101100\times 2^{10}=(2^0+2^{-1}+2^{-3}+2^{-4}+2^{-5}+2^{-7}+2^{-8})\times 2^{10}=2^{10}+2^9+2^7+2^6+2^5+2^3+2^2={1772}_{10}$

• 指数部は、バイアスを考慮して $2^{10}=2^{25-15}=2^{{11001}_2-15}$ なので、 11001 と符号化される。

IEEE 754半精度浮動小数点数形式: 0　11001　1011101100
10進数: 1772

解説

3.32の計算だと、ガード桁以降の 011 を1度しか加えられなかったが、3.33の計算だと 011 を2度加えられたので、最後の桁上げに寄与できた。

3.34

問題

問題3.32および3.33の解答から，$(3.984375\times {10}^{-1}+3.4375\times {10}^{-1})+1.771\times {10}^3=3.984375\times {10}^{-1}+(3.4375\times {10}^{-1}+1.771\times {10}^3)$ は成立するか．

解答

成立しない。

解説

一般に、桁落ちの可能性があるので、浮動小数点数の和には交換法則は成り立たない。

3.35

問題

$(3.41796875\times {10}^{-3}\times 6.34765625\times {10}^{-3})\times 1.05625\times {10}^2$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

解答

• 10のべき乗部分が残っていると2進数に変換するときに邪魔なのでなくす。

  • $3.41796875\times {10}^{-3}=0.00341796875$
  • $6.34765625\times {10}^{-3}=0.00634765625$
  • $1.05625\times {10}^2=105.625$

• 2進数に変換する。

  • $0.00341796875={0.00000000111}_2$
  • $0.00634765625={0.00000001101}_2$
  • $105.625={1101001.101}_2$

• 正規化する。

  • $0.00000000111=1.11\times 2^{-9}$
  • $0.00000001101=1.101\times 2^{-8}$
  • $1101001.101=1.101001101\times 2^6$

• まずは $3.41796875\times {10}^{-3}\times 6.34765625\times {10}^{-3}={1.11}_2\times 2^{-9}\times {1.101}_2\times 2^{-8}$ の計算をする。

• 積の指数部は $2^{-9}\times 2^{-8}=2^{-17}$

• 仮数部はともに10ビットに収まる。

• 仮数部の積を筆算する。

  1 2 3 4 5 6 7 8

  1.11 x 1.101 --------- 1 110 111 0 1110 --------- 10110 110

• 結果は $10.11011\times 2^{-17}=1.011011\times 2^{-16}$ 。仮数部10ビットに収まっている。

• これと $105.625={1.101001101}_{\times }{2}^6$ の積を取る。

• 積の指数部は $2^{-16}\times 2^6=2^{-10}$ 。

• 仮数部の積を筆算する。

  1 2 3 4 5 6 7 8 9 10 11

  1.0110110 1.101001101 ------------------ 1 011011000 101 1011000 1011 011000 1011011 000 101101100 0 1011011000 -------------------- 10010110001 011111000

• 指数部まで含めた結果は $10.010110001011111000\times 2^{-10}=1.0010110001011111000\times 2^{-9}$ 。

• 仮数部10ビット、ガード桁1ビット、丸め桁1ビット、スティッキービット1ビットまで削ると、結果は $1.0010110001011\times 2^{-9}$ となる。（スティッキービットは、13ビット目以降の 1111000 に1つ以上1が立っているので1となる。）

• ガード桁以降は $\frac{1}{4}+\frac{1}{8}=\frac{3}{8}\mathrm{u}\mathrm{l}\mathrm{p}$ なので切り捨てられ、最終ビットは1のまま。

• 10進数で表すと $1.0010110001\times 2^{-9}=(2^0+2^{-3}+2^{-5}+2^{-6}+2^{-10})\times 2^{-9}=2^{-9}+2^{-12}+2^{-14}+2^{-15}+2^{-19}=0.0022907257080078125$

• 指数部は、バイアスを考慮して $2^{-9}=2^{6-15}=2^{{00110}_2-15}$ なので、 00110 と符号化される。

IEEE 754半精度浮動小数点数形式: 0　00110　0010110001
10進数: 0.0022907257080078125

解説

電卓で計算した場合の結果は 0.0022916495800018307 であり、有効数字3桁の範囲で一致。

3.36

問題

$3.41796875\times {10}^{-3}\times (6.34765625\times {10}^{-3}\times 1.05625\times {10}^2)$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

解答

• 3.35と同様に正規化して、

  • $3.41796875\times {10}^{-3}={1.11}_2\times 2^{-9}$
  • $6.34765625\times {10}^{-3}={1.101}_2\times 2^{-8}$
  • $1.05625\times {10}^2={1.101001101}_2\times 2^6$

• まずは $6.34765625\times {10}^{-3}\times 1.05625\times {10}^2={1.101}_2\times 2^{-8}\times {1.101001101}_2\times 2^6$ の計算をする。

• 積の指数部は $2^{-8}\times 2^6=2^{-2}$

• 仮数部はともに10ビットに収まる。

• 仮数部の積を筆算する（筆算が縦に長くなると大変なので順序を変えます😅）。

  1 2 3 4 5 6 7 8

  1.101001101 x 1.101 --------------------- 1101001 101 110100110 1 1101001101 --------------------- 10101011101 001

• 結果は $10.101011101001\times 2^{-2}1.0101011101001\times 2^{-1}$ 。計算途中なので、ガード桁、丸め桁、スティッキービットは保持できる。

• これと $3.41796875\times {10}^{-3}={1.11}_2\times 2^{-9}$ の積を取る。

• 積の指数部は $2^{-9}\times 2^{-1}=2^{-10}$ 。

• 仮数部の積を筆算する（また順序を変えます😉 ）。

  1 2 3 4 5 6 7 8

  1.0101011101 001 x 1.11 ------------------------------ 101010111010 01 1010101110100 1 10101011101001 ------------------------------ 100101100010111 11

• 指数部まで含めた結果は $10.010110001011111\times 2^{-10}=1.0010110001011111\times 2^{-9}$ 。

• これは 3.35 と全く同じなので、下記を得る。

IEEE 754半精度浮動小数点数形式: 0　00110　0010110001
10進数: 0.0022907257080078125

解説

乗算の場合、途中で桁数が膨れ上がるが、有効数字外の桁はスティッキービットに1が立っていることでのみ表現できる。

3.37

問題

問題3.35および3.36の解答から，$(3.41796875\times {10}^{-3}\times 6.34765625\times {10}^{-3})\times 1.05625\times {10}^2=3.41796875\times {10}^{-3}\times (6.34765625\times {10}^{-3}\times 1.05625\times {10}^2)$ は成立するか．

解答

成立する。

解説

特になし。

3.38 (未回答)

問題

$1.666015625\times {10}^0\times (1.9760\times {10}^4+-1.9744\times {10}^4)$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

3.39 (未回答)

問題

$(1.666015625\times {10}^0\times 1.9760\times {10}^4)+(1.666015625\times {10}^0\times -1.9744\times {10}^4)$ を手作業で計算せよ．ただし，2つのデータは，問題3.27（および本文）で説明した，16ビットの半精度形式で格納されているものとする．ガード桁と丸め桁とスティッキー・ビットがそれぞれ1ビットあり，最も近い偶数へ丸めるものとする．すべてのステップを示せ．答えを16ビットの浮動小数点形式と10進数の両方で示せ．

3.40 (未回答)

問題

問題3.38および3.39の解答から，$1.666015625\times {10}^0\times (1.9760\times {10}^4+-1.9744\times {10}^4)=(1.666015625\times {10}^0\times 1.9760\times {10}^4)+(1.666015625\times {10}^0\times -1.9744\times {10}^4)$ は成立するか．

3.41

問題

IEEE浮動小数点形式を使用して，－1/4を表すビット・パターンを示せ．－1/4を正確に表すことができるか．

単精度浮動小数点形式と解釈する。

解答

1　01111101　00000000 00000000 0000000

このビットパターンは $-\frac{1}{4}$ を正確に表している。

解説

• 符号ビットは1。
• 2進数で正規化して、$\frac{1}{4}=0.01=1.0\times 2^{-2}$ 。
• 指数部は、バイアスを考慮して $2^{-2}=2^{125-127}=2^{{1111101}_2-127}$ なので、 1111101 と符号化される。

3.42

問題

－1/4を4回加算したら，どんな答えが得られるか．（－1/4）×4の答えはどうなるか．両者は同じか．両者はどうあるべきか．

解答

• $(-\frac{1}{4})+(-\frac{1}{4})+(-\frac{1}{4})+(-\frac{1}{4})=-1\times 2^0$
• $(-\frac{1}{4})\times 4=-1\times 2^0$

両者は同じ。同じであるべき。

解説

• $(-\frac{1}{4})+(-\frac{1}{4})+(-\frac{1}{4})+(-\frac{1}{4})$ の計算:
  • 正規化済みの表現は $1.0\times 2^{-2}$ 。
  • まず2回足して、 $1.0\times 2^{-2}+1.0\times 2^{-2}=10.0\times 2^{-2}=1.0\times 2^{-1}$ 。
  • もう一度足して、 $1.0\times 2^{-1}+1.0\times 2^{-2}=(1.0+0.1)\times 2^{-1}=1.1\times 2^{-1}$ 。
  • 最後にもう一度足して、 $1.1\times 2^{-1}+1.0\times 2^{-2}=(1.1+0.1)\times 2^{-1}=10.0\times 2^{-1}=1\times 2^0$
• $(-\frac{1}{4})\times 4$ の計算:
  • 4を正規化して、 $100=1.0\times 2^2$
  • ${1.0}_2\times 2^{-2}\times 1.0\times 2^2=1.0\times 2^0$

3.43

問題

値1/3の仮数のビット・パターンを示せ．ただし，仮数部の形式は浮動小数点2進数とする．仮数部の長さは24ビットとし，正規化する必要はない．その表現は正確か．

暗黙の1もないものと解釈する。

解答

仮数のビットパターンは 00101010 10101010 10101010 。正確ではない。

解説

• 2進小数表現を考える。
  • $\frac{1}{3}=\frac{1}{4}+x$ としたとき、 $x=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$。
  • $\frac{1}{12}=\frac{1}{16}+x$ としたとき、 $x=\frac{1}{12}-\frac{1}{16}=\frac{1}{48}$。
  • この要領で繰り返すと、 $\frac{1}{3}=\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\dots =0.010101{\dots }_2$ という循環小数であることがわかる。
• 循環小数なので、有限のビット数では正確に表すことができない。

3.44

問題

値1/3の仮数のビット・パターンを示せ．ただし，仮数部には2進数の代わりにバイナリ・コード化した10進数（基数2）を使用するものとする．仮数部の長さは24ビットとし，正規化する必要はない．その表現は正確か．

先頭に暗黙の 0. が付くものとする。

解答

仮数のビットパターンは 0011 0011 0011 0011 0011 0011 。正確ではない。

解説

バイナリコード化した10進数というのは以下の表現形式である。

（通貨など、十進数で小数点以下を正確に扱いたい際に使う符号方式である。）

10進数で表しても $\frac{1}{3}=0.33333\dots$ と循環小数になるので、ビットパターンとしても循環する。

3.45

問題

値1/3の仮数のビット・パターンを示せ．ただし，仮数部には2進数の代わりに基数が15の数を使用するものとする（基数が16の数では各数字を0～9およびA～Fで表すが，基数が15の数では0～9およびA～Eを使用する）．仮数部の長さは24ビットとし，正規化する必要はない．その表現は正確か．

先頭に暗黙の 0. が付くものとする。

解答

0101 0000 0000 0000 0000 0000 。正確。

解説

• 15進小数表現を考える。
  • $\frac{1}{3}=\frac{5}{15}$ なので、 ${0.5}_{15}$ と表記できる。
• バイナリコード化を考えると、4bitで 0~E を表せるので、先頭に暗黙の 0. があれば 0101 0000... と表せる。

3.46

問題

値1/3の仮数のビット・パターンを示せ．ただし，仮数部には2進数の代わりに基数が30の数を使用するものとする（基数が16の数では各数字を0～9およびA～Fで表すが，基数が30の数では0～9およびA～Tを使用する）．仮数部の長さは20ビットとし，正規化する必要はない．その表現は正確か．

先頭に暗黙の 0. が付くものとする。

解答

01010 00000 00000 00000 。正確。

解説

• 30進小数表現を考える。
  • $\frac{1}{3}=\frac{10}{30}$ なので、 $0.A_{30}$ と表記できる。
  • バイナリコード化を考えると、5bitで 0~T を表せるので、先頭に暗黙の 0. があれば 01010 00000... と表せる。

3.47

問題

下のＣコードは，入力配列sig_in上で，4項からなる有限インパルス応答を実現する．配列中の値はすべて，16ビットの固定小数点形式であるとする．

1
2

for (i = 3; i < 128; i++)
  sig_out[i] = sig_in[i - 3] * f[0] + sig_in[i - 2] * f[1] + sig_in[i - 1] * f[2] + sig_in[i] * f[3];

SIMD命令と128ビットのレジスタを備えたプロセッサ上で，このコードを最適化したアセンブリ・コードを書くと想定する．ただし，命令セットの詳細は分からないものとする．半語並列性を最大限に活用し，レジスタとメモリの間で移送されるデータ量を最小限に抑えるようにして，このコードをどのように実現したらよいか，簡単に説明せよ．使用する命令に関する，すべての想定を記述せよ．

解答

• 使用する命令の想定:
  • dotph : 1個の入力レジスタ(128ビット)の上位64ビットに4個の半精度固定小数点数から成るベクトル、下位64ビットに別の4個の半精度固定小数点数から成るベクトルが入った状態で、それらの内積を取って、結果の半精度固定小数点数を出力レジスタ(128ビット)の16ビットごと全域に格納する。
    • ${\mathbf{R}}_{in;127-64}\cdot {\mathbf{R}}_{in;63-0}={\mathrm{R}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$
    • ${\mathbf{R}}_{in;127-64}=(a_1,a_2,a_3,a_4)$
    • ${\mathbf{R}}_{in;63-0}=(b_1,b_2,b_3,b_4)$
    • ${\mathbf{R}}_{out}=(a_1{b}_1+a_2{b}_2+a_3{b}_3\dots +a_4{b}_4,\dots )$
  • loadph : 入力レジスタ(128ビット)に、指定したメモリアドレスから、連続する8個の半精度固定小数点数をロードする。
  • storesh : 入力レジスタ(128ビット)の末尾16ビットを、指定したメモリアドレスにストアする。
  • sll : 論理左シフト。
  • srl : 論理右シフト。
  • andph : 論理積。
  • orph : 論理積。

この上で、ベクトル化した擬似コードを示す。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

loadph(R1, f);   // レジスタR1に (??, ??, ??, ??, f[3], f[2], f[1] f[0]) をロード
sll(R1, R1, 8);  // R1 = R1 << 8byte = (f[3], f[2], f[1], f[0], ??, ??, ??, ??)
andph(R1, R1, 0xFFFFFFFFFFFFFFFF0000000000000000);  // R1 = R1 & 0xFFFFFFFFFFFFFFFF0000000000000000 = (f[3], f[2], f[1], f[0], 0, 0, 0, 0)

for (i = 3; i < 128; i += 4) {
  loadph(R2, &sig_in[i-3]);  // レジスタR1に (sig_in[i+4], sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i], sig_in[i-1], sig_in[i-2], sig_in[i-3]) をロード

  srl(R3, R2, 2);          // R3 = R2 >> 2byte = (??, sig_in[i+4], sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i], sig_in[i-1], sig_in[i-2])
  andph(R3, R3, 0x0000000000000000FFFFFFFFFFFFFFFF);  // R3 = R3 & 0x0000000000000000FFFFFFFFFFFFFFFF = (0, 0, 0, 0, sig_in[i+1], sig_in[i], sig_in[i-1], sig_in[i-2])
  orph(R3, R3, R1);        // R3 = R3 | R1 = (f[3], f[2], f[1], f[0], sig_in[i+1], sig_in[i], sig_in[i-1], sig_in[i-2]);
  dotph(R3, R3);           // R3 = R3_{127-64} dot R3_{63-0} = f[3] sig_in[i+1] + f[2] sig_in[i] + f[1] sig_in[i-1] + f[0] sig_in[i-2]
  storesh(&sig_out[i+1], R3);

  srl(R4, R2, 2);          // R4 = R2 >> 4byte = (??, ??, sig_in[i+4], sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i], sig_in[i-1])
  andph(R4, R4, 0x0000000000000000FFFFFFFFFFFFFFFF);  // R4 = R4 & 0x0000000000000000FFFFFFFFFFFFFFFF = (0, 0, 0, 0, sig_in[i+2], sig_in[i+1], sig_in[i], sig_in[i-1])
  orph(R4, R4, R1);        // R4 = R4 | R1 = (f[3], f[2], f[1], f[0], sig_in[i+2], sig_in[i+1], sig_in[i], sig_in[i-1]);
  dotph(R4, R4);           // R4 = R4_{127-64} dot R4_{63-0} = f[3] sig_in[i+2] + f[2] sig_in[i+1] + f[1] sig_in[i] + f[0] sig_in[i-1]
  storesh(&sig_out[i+2], R4);

  srl(R5, R2, 2);          // R5 = R2 >> 4byte = (??, ??, ??, sig_in[i+4], sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i])
  andph(R5, R5, 0x0000000000000000FFFFFFFFFFFFFFFF);  // R5 = R5 & 0x0000000000000000FFFFFFFFFFFFFFFF = (0, 0, 0, 0, sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i])
  orph(R5, R5, R1);        // R5 = R5 | R1 = (f[3], f[2], f[1], f[0], sig_in[i+3], sig_in[i+2], sig_in[i+1], sig_in[i]);
  dotph(R5, R5);           // R5 = R5_{127-64} dot R5_{63-0} = f[3] sig_in[i+3] + f[2] sig_in[i+2] + f[1] sig_in[i+1] + f[0] sig_in[i]
  storesh(&sig_out[i+3], R5);

  andph(R2, R2, 0x0000000000000000FFFFFFFFFFFFFFFF);  // R2 = R2 & 0x0000000000000000FFFFFFFFFFFFFFFF = (0, 0, 0, 0, sig_in[i], sig_in[i-1], sig_in[i-2], sig_in[i-3])
  orph(R2, R2, R1);        // R2 = R2 | R1 = (f[3], f[2], f[1], f[0], sig_in[i], sig_in[i-1], sig_in[i-2], sig_in[i-3]);
  dotph(R2, R2);           // R2 = R2_{127-64} dot R2_{63-0} = f[3] sig_in[i] + f[2] sig_in[i-1] + f[1] sig_in[i-2] + f[0] sig_in[i-3]
  storesh(&sig_out[i], R2);
}

解説

• 内積計算の際、R2の計算は最後に回す。R2はR3~R5の入力にも使われるので。